I believe most of you who have followed Dan Brown's "The Da Vinci's Code" story closely would be familiar with; or at least heard of it more than just once - Phi, the golden ratio.
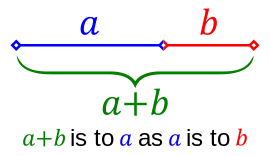
In spite of its significance in mathematics and arts, the definition of a golden ratio is rather simple actually. Take one line here, and then we cut the line into two segments in different length in a special way. Say we name the longer line segment as line segment a, and the shorter one, b.
What is so special with it is that we have to make sure the ratio of the length of the entire line (a + b) to the length of the longer line segment (a), is the same with the ratio of the length of the longer line segment (a) to the shorter one (b). Get that right, and we will already be looking at the magic number, the golden ratio, a.k.a. Phi.
The golden ratio is often denoted by the Greek letter phi (Φ or φ). Phi is a ratio, and moreover, an irrational mathematical constant; which approximately equals to 1.6180339887. When expressed algebraically:
In one of his books, Stephen Hawking once mentioned the more numbers of mathematical formulas are printed in a book, the less popular it will be selling. Thus let's leave that algebraic expression as the one and only mathematical formula you will see in this article, to prevent further boredom. :)
Well, back to the heart-gripping fiction. The handsome Harvard lecturer Robert Langdon gave a mathematics lecture on golden ratio in his class, trying to tell his students how special, and how really close the number is, to human beings. Fibonacci's sequence, ratio of female bees to male bees in a hive, ratio of one spiral to the next spiral on a nautilus, ratio of the diameter of a rotation to the next in a sunflower's growth, even to the ratio between different human body parts.
"Measure the distance from the tip of your head to the floor. Then divide that by the distance from your belly button to the floor. Guess what number you get," says Langdon in the class. And we don't have to guess like his students here; the answer by Langdon, is Phi; no surprise here. To top it off, he claims that Leonardo da Vinci has shown belief in golden ratio as the ratio of the height of a perfect human face to its width; that the artist used Phi in his artwork, Vitruvian Man. - Discovermagazine.com
Of course, we have much to thank Langdon, or Brown, for indirectly giving such a mathematical revelation to the readers who may or may not know about Phi before. However, Brown is a fiction writer, and there are certainly a lot of disputable claims in this book; and some are more fiction than fact. And thus as critical-thinking readers, we have to ask: how much are the claims about Phi is true in the story?
Look at the human body proportion example Langdon proposes. Measure the distance from the tip of your head to the floor. Then divide that by the distance from your belly buttion to the floor. What answers, we will actually get? I bet it's something close to 1.6. But what is 1.6? When we compare the number 1.6, to the irrational number of Phi, 1.6180339887... , we can see why this claim is impractical, weak in foundation. There are a lot of ratios we can get that, when simplified, is 1.6. But that can be derived from a numerous possibility of exact numbers - 1.623, 1.607, 1.572, etc. And these numbers I just gave as examples cannot be said to be anywhere close to 1.6180339887... . - Discovermagazine.com
Besides, if you spend time measuring your body parts, you might get numbers like 1.2, 1.8, other than 1.6. It's more coincidence than predetermined. - Discovermagazine.com
Similarly, the claims on Vitruvian Man doesn't seem to be very solid either. According to , the equally common claims that Sandro Botticelli used φ to proportion Venus in his famous painting The Birth of Venus and that Georges Seurat based his painting The Side Show on φ, are also seem to be without foundation. Painters who definitely did make use of φ include the 20th-century artists Louis-Paul-Henri Sérusier, Juan Gris, Gino Severini, and Salvador Dalí; but all four seem to have been experimenting with φ for its own sake rather than for some intrinsic aesthetic reason. - Discovermagazine.com
Knowing this much, it's probably time to examine how much facts are there in your knowledge about Phi. And we've got a cool quiz here (from "Cracking the Da Vinci Code", Discovermagazine.com ) :
A GOLDEN RATIO QUIZ
There are so many false claims made about the golden ratio, and so many surprising truths, that it can be hard to separate fact from fiction. Here are some of the most common statements you will find in the literature, besides the ones mentioned in the article. See how many you can correctly guess are true or false. (True means known for sure to be true; false means there is insufficient evidence to justify the statement.)
1. The Egyptian pyramids were constructed using the golden ratio.
2. Some Egyptian tombs were constructed using the golden ratio.
3. Some stone tablets show the Babylonians knew about the golden ratio.
4. The cubists based much of their work on the golden ratio.
5. The famous French architect Le Corbusier advocated and used the golden ratio in architecture.
6. The Secretariat building at the United Nations headquarters in New York comprises a stack of three golden rectangles.
7. Some Gregorian chants are based on the golden ratio.
8. Mozart used the golden ratio in some of his music.
9. Béla Bartók used the golden ratio in some of his music.
10. When a falcon attacks its prey, it swoops in along a path that is mathematically related to the golden ratio.
11. The poet Virgil based the meter of his poem The Aeneid on the golden ratio.
12. Some 12th-century Sanskrit poems have a meter based on the Fibonacci sequence (and hence are related to the golden ratio).
13. The golden ratio occurs in certain crystal structures.
14. There is a Fibonacci number with exactly 666 digits.
15. If you square any Fibonacci number, the answer will differ by at most 1 from the product of the two adjacent Fibonacci numbers.
Answers:
1. F 2. F 3. F 4. F 5. T 6. F 7. F 8. F 9. F 10. T 11. F 12. T 13. T 14. T 15. T
Now I'm sure you have a clearer, more-examined, less-disputable views about Phi. Although there is a lot of claims in Brown's novel that seems to lack viable justification, but a few points Langdon proposes are true anyway. At least the part about plants.
According to Devlin, to achieve maximum efficiency, flower heads and plant leaves grow in a spiral fashion governed by the golden ratio. Since φ is an irrational number and the number of petals, spirals, or stamens in any plant or flower has to be a whole number, nature “rounds off” to the nearest whole number. - Discovermagazine.com
He also explained that in the case of leaves, each new leaf is added so that it least obscures the leaves already below and is least obscured by any future leaves above it. Hence the leaves spiral around the stem. For seeds in the seed head of a plant, nature wants to pack in as many as possible. The way to do this is to add new seeds in a spiral fashion. - Discovermagazine.com
As such, we come to see why Phi is so significant in science - it's the ratio that gives optimal solution to plant growth equations. - Discovermagazine.com
Like how Devlin puts it, "It’s a question of nature being efficient".As readers living in a society "exquisitely dependent" on science and technology, we have to sharpen our eyes and logical senses when we read. I certainly do not hope people in our era live up to fulfill Dr. Carl Sagan's expectation that "hardly anyone knows anything about science and technology".
Hence we just have to be critical, and check, and double-check every fact we are absorbing.
"There are many hypotheses in science which are wrong. That's perfectly all right; they're the aperture to finding out what's right. Science is a self-correcting process. To be accepted, news ideas must survive the most rigorous standards of evidence and scrutiny."
And there we go, Dr. Sagan's quote has quite sum the whole thing up. :)
*Dr. Carl Sagan, 1934-1996, American astronomer, writer and scientist.

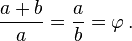




0 comments:
Post a Comment